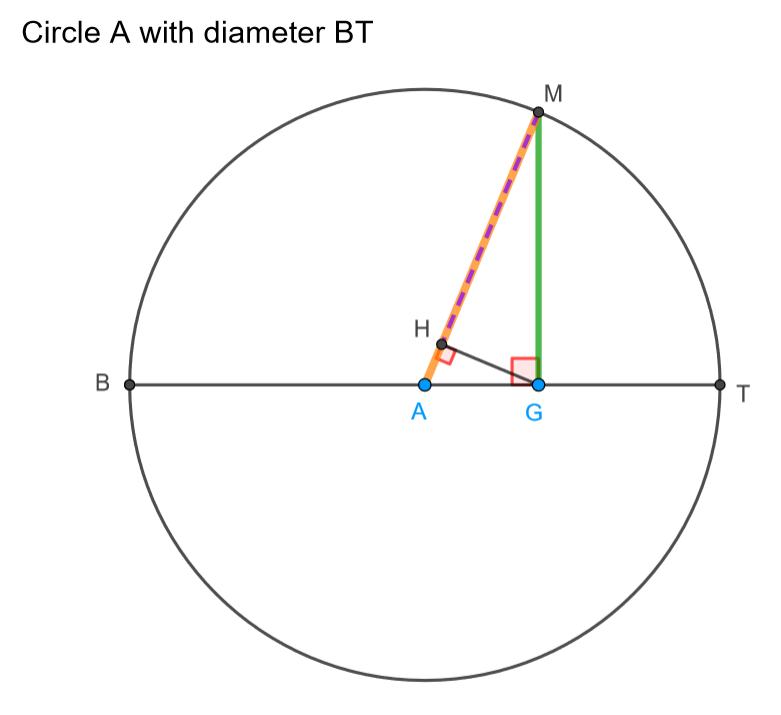
Here we can see all three Pythagorean Means (arithmetic mean, geometric mean, harmonic mean) interacting in a circle. We are taking the means of the two numbers BG and GT which make up the diameter.
What’s going on: Given circle centered at A, segment GM perpendicular to the diameter. In right triangle AGM, segment GH is an altitude to the hypotenuse. Show that AM is the arithmetic mean of GB and GT, HM is the harmonic mean of GB and GT, and GM is the geometric mean of GB and GT.
Student handout: The-Three-Pythagorean-Means-in-a-Circle
GeoGebra file: here
TEACHER NOTES
This is a very rich diagram. As point G moves to the left, making the two quantities nearer and nearer to equal, we see the 3 means getting nearer to equal — and equality can be achieved. The key to the proof is drawing in the triangle (BMT) inscribed in the semicircle. The proofs then follows from the high school geometry theorems involving an altitude drawn to the hypotenuse of a right triangle.
Important/Useful Takeaways for students:
- The three means, arithmetic mean, geometric mean, harmonic mean, each have uses in the real world. Research this.
- Arithmetic mean ≤ geometric mean ≤ harmonic mean.
- The diagram is a good way to see numerical relationships.
