What’s going on: Given two segments (telephone poles) perpendicular to a common line and the diagonals from their endpoints, prove that the perpendicular segment from the point of intersection of the diagonals to the common line is 1/2 the harmonic mean of the original segments (telephone poles).

Student handout: Harmonic-Mean-Between-Telephone-Poles

GeoGebra file: here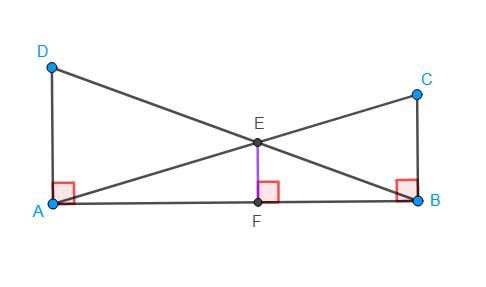

TEACHER NOTES

There are two sets of similar triangles, and EF is a common segment. One way to prove this is to set up two proportions, each containing EF. The proportions can be combined and algebra can be applied to find the result.

Important/Useful Takeaways for students:

  • The similar triangles here give us helpful proportions, but then we need to use algebra find the harmonic mean.
  • Harmonic mean of a and b = \frac{2ab}{a+b}

The harmonic mean of two numbers is an interesting mean. The harmonic mean is smaller than the arithmetic mean. We will see that the harmonic mean is more ubiquitous than we might think. \frac{2ab}{a+b}