Harmonic Mean in Trapezoid

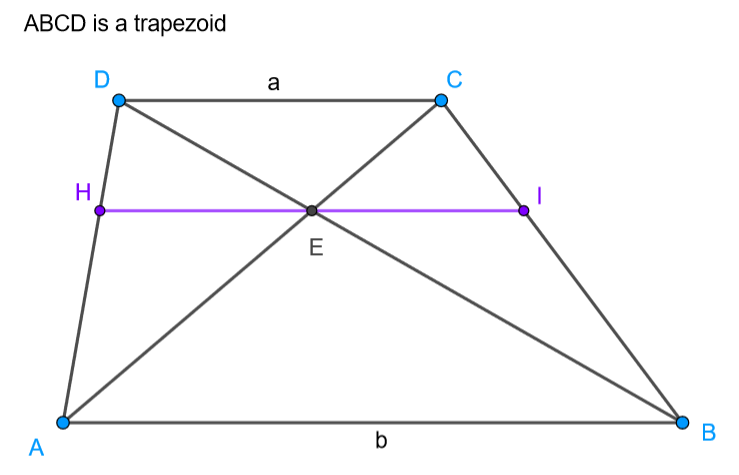
What’s going on: Here we have a trapezoid and its diagonals. The segment parallel to the bases which passes through the intersection of the the diagonals is the harmonic mean of the lengths of the bases.

Student handout: HarmonicMeanInTrapezoid

GeoGebra file: here

 

TEACHER NOTES

There are (at least) three sets of similar triangles. It is quite striking that HE and EI are congruent (making E a midpoint) with no congruent triangles in the figure. To prove this we want HI in terms of the length of the bases, a and b. This can be done by setting up proportions and combining them. When setting up the ratios both of the following may be useful (1) top-portion-to-bottom-portion ratios (which are a/b) and (2) top-portion-to-‘whole-thing’ ratios (which are a/(a+b)).

Important/Useful Takeaways for students:

• The similar triangles give us helpful proportions. Then the power of algebra gives us many results.
• Proportions are quite easy to manipulate (with practice).  There are useful properties of proportions.
  

The harmonic mean of two numbers is an interesting mean. The harmonic mean is smaller than the arithmetic mean. We will see that the harmonic mean is more ubiquitous than we might think.